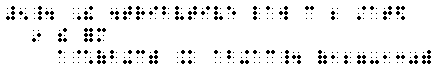Format

1. A line must not be skipped above or below a displayed expression unless the expression precedes or follows a heading, or unless a blank line is required under other provisions of the code.

2. When a displayed expression occurs in unitemized explanatory portions of the text, it must begin in cell 3, and its runovers must begin in cell 5.

   (1) The expression a(b + c) -d(b + c) has the
   form ax - dx where x = b + c. Thus

    ax - dx = x(a - d)

   and therefore

   a(b + c) - d(b + c) = (b + c)(a - d).

   

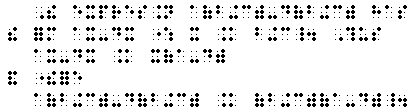
   (2) A sequence a₁, a₂, a₃, ..., a_n is said to
   converge if, for each h > 0, there exists
   a positive number M such that
   | a_n-A | < h, for all n > M.

   A sequence that does not converge is said
   to diverge.

   

   (3) We use the number line to show

   -6 < -5, 0 < +6, -8 < +2, -1 > -5, +1 > -1.

   Is every positive integer greater than 0? Is
   every negative integer less than 0?

   

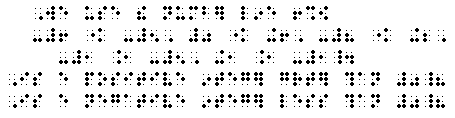
   (4) The equation states that the
   product of 24 and some number     24 x N = 264
   is 264. How can you find the
   missing numeral?

   

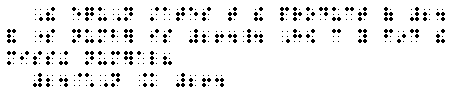
3. When a displayed expression occurs within itemized text and the item containing it is a main division with no substitutions, the displayed expression must begin in cell 5, and its runovers must begin in cell 7.

   (1) If A, B, C, C' are constants, show that

   Ax + By + C = 0
   Ax + By + C' = 0

   are parallel and the lines

   Ax + By + C = 0
   Ax + By + C' = 0

   are perpendicular.

   

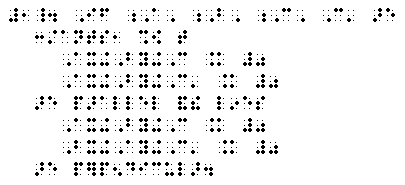
   (2) To find the product of 2 x 5.4

   First: multiply the tenths, 2 x .4 = .8,
   Second: multiply the ones, 2 x 5 =10.

   Then add: 10 + .8 = 10.8.

   

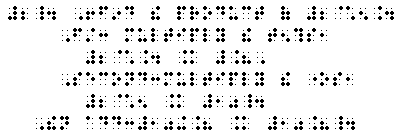
   (3). Use the number line to show

   -1 < +1, -5 < -1, +12 > -8, +6 > +4.

   If every negative integer is less than 0,
   what is every positive integer?

   

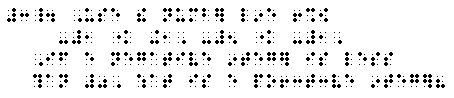
4. When a displayed expression occurs within itemized text and the item containing it is a main division with subdivisions, the displayed expression, regardless of whether it applies to the main division or a subdivision, must begin in cell 7, and its runovers must begin in cell 9.

   (1) Write each positive integer as a polynomial in 10.

   1. Compare

      x³ + 9x² + 7x + 1 and
      10³ + 9(10)² + 7(10) + 1, that is 1971.

   2. The number 185,000,000,000 can be written as
      185 x 10⁹, or as 1.85 x 10¹¹.

    Use the principles in a and b to write
    x⁴ + 7x³ + 5x² + 3x + 1 and 125,000,000,000.

   

5. When a number or letter is used to identify a displayed expression, it must begin in the appropriate cell for displayed material in accordance with the rules of a-d above. If such numbers or letters occur to the right of the expression in print, they must be placed at the left of the expression in braille, and a transcriber's note concerning the change in position must be incorporated at the beginning of the first volume.

   A page reference to a displayed expression must immediately follow that expression.

   (1) Two basic laws of arithmetic are the
   commutative law for addition
   a + b = b + a, (1)

   and the commutative law for multiplication
   a x b = b x a. (2).

   

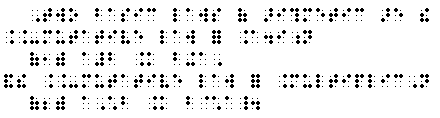
   (2) Use the formula

   a_n = a₁ + (n-1)d  (12.3)
   to find a_n and n when a₁ = 1, d = 7, s_n = 204.

   

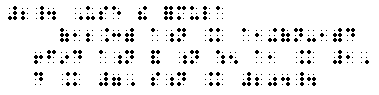
   (3) Give two examples illustrating

   (a) The associative law for addition
   (a + b) + c = a + (b + c).   (4)
   (b) The associative law for multiplication
   (a x b) x c = a x (b x c).  (5).

   

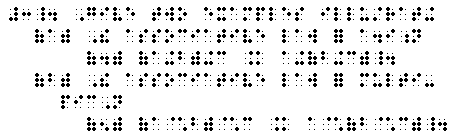
   (4) The rules for subtraction depend upon those for addition

   a - b = a + (-b).  (115-116)

   

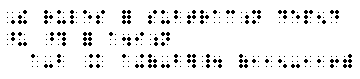
   (5) The distributive law can be stated in the form

   a x (b + c) = ab + ac.  (127-130).